กลศาสตร์คลื่น

ผลงานของเดอบรอยล์และไฮเซนเบิร์กได้นำไปสู่แนวความคิดของการสร้างทฤษฎีใหม่ขึ้นมาสำหรับอธิบายเกี่ยวกับอิเล็กตรอนในอะตอมดังนี้

1. อาศัยสมบัติความเป็นคลื่นของอิเล็กตรอน จึงวิเคราะห์หาสมบัติต่างๆของอิเล็กตรอนโดยการสร้างสมการคลื่น (wave equation) แล้วแก้สมการเพื่อหาค่าต่างๆออกมา

2. เนื่องจากอิเล็กตรอนมีขนาดเล็กมาก สมบัติต่างๆของอิเล็กตรอนจะวัดได้ในระดับโอกาส หรือความน่าจะเป็น (probability) ที่จะพบอิเล็กตรอนที่บริเวณต่างๆรอบนิวเคลียส หรือความหนาแน่นของอิเล็กตรอน (electron density) ที่บริเวณต่างๆรอบนิวเคลียส

        ชเรอดิงเจอร์ ได้เสนอสมการคลื่นโดยใช้สัญลักษณ์ต่างๆดังนี้

Hy  =   E y

• y คือ สัญลักษณ์ของฟังก์ชันคลื่น (wave function) เรียกว่า psi เป็นฟังก์ชันทางคณิตศาสตร์ที่เกี่ยวข้องกับความเป็นคลื่นของอิเล็กตรอน ค่า yไม่มีความหมายทางฟิสิกส์ แต่ค่า y²เกี่ยวข้องกับโอกาสที่จะพบอิเล็กตรอนที่จุดๆหนึ่ง หริอ ความหนาแน่นของอิเล็กตรอนที่จุดนั้นๆ y² d_x d_y d_z ดังนั้น y² ก็คือโอกาสหรือความน่าจะเป็นของการที่จะพบอิเล็กตรอนที่จุดหนึ่งภายในปริมาตรจำนวนหนึ่งรอบๆนิวเคลียส




• H เรียกว่าแฮมิลโตเนียน (hamiltonian)ของระบบ ความหมายอย่างง่าย ๆ คือ เป็นตัวบ่งถึงลักษณะแวดล้อม สมบัติทางพลังงานจลน์และพลังงานศักย์ของอิเล็กตรอน เช่น ถ้าระบบเป็น He⁺ ในระบบประกอบด้วยนิวเคลียสซึ่งมีโปรตอน 2 ตัว และนิวตรอน 2 ตัว โดยมีอิเล็กตรอน 1 ตัว เคลื่อนที่อยู่รอบๆนิวเคลียส แฮมิลโตเนียนของอิเล็กตรอนตัวนี้จะเป็นเทอมซึ่งบ่งถึงพลังงานจลน์เนื่องจากการเคลื่อนที่รอบนิวเคลียส และมีพลังงานศักย์ เพราะถูกดึงดูดกับโปรตอนที่อยู่ในนิวเคลียส แต่ถ้าระบบเป็น He อะตอม แฮมิลโตเนียนของอิเล็กตรอนตัวหนึ่งๆ (อิเล็กตรอนทั้งสองตัวจะเหมือนกันทุกประการ) จะบ่งถึงพลังงานจลน์และพลังงานศักย์ โดยที่พลังงานศักย์จะประกอบด้วยแรงดึงดูดกับนิวเคลียสและแรงผลักระหว่างอิเล็กตรอนด้วยกัน

• E คือ พลังงานของอิเล็กตรอนตัวที่กำลังศึกษานั้น

การแก้สมการคลื่น

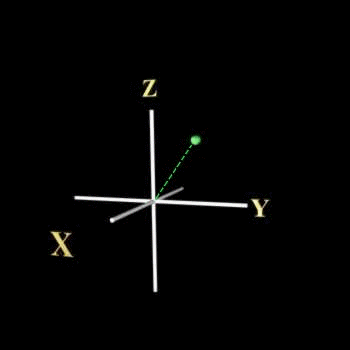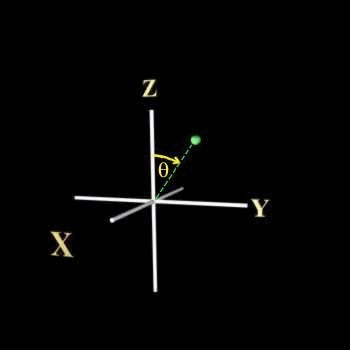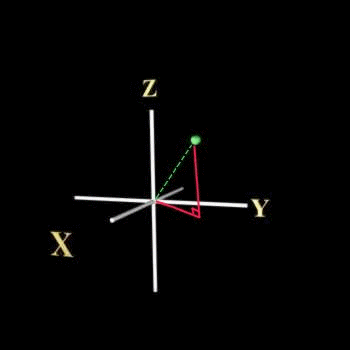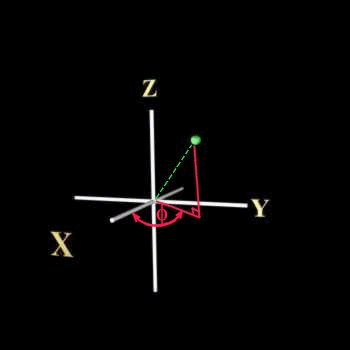
แกน x,y,z ตั้งฉากซึ่งกันและกันใช้แกนแบบ spherical polar coordinates ซึ่งมีตัวแปรเป็น r,q,f

ในการแก้สมการคลื่นจะแยกฟังก์ชันคลื่นออกเป็น 2 ส่วนใหญ่ๆ คือ

y(r, q, f) = R(r) Y( q, f)

• R(r) เรียกว่า ส่วนเชิงรัศมี
• Y( q, f) เรียกว่า ส่วนเชิงมุม

จากการแก้สมการของชเรอดิงเจอร์ พบว่าฟังก์ชันคลื่นของอิเล็กตรอน นอกจากจะขึ้นกับตัวแปร (r, q,f) แล้วยังขึ้นกับเลขจำนวนเต็มอื่นอีกดังนี้

ส่วนเชิงรัศมีขึ้นกับค่า n,l

R(r) = R_{n, l}(r)

ส่วนเชิงมุมขึ้นกับค่า l, m_l

Y( q, f) = Y_{l, ml}( q, f)

โดยที่ n, l, m_l เป็นเลขจำนวนเต็ม