| ออร์บิทัลอะตอม |
![]() ออร์บิทัลอะตอม
ออร์บิทัลอะตอม
![]() ออร์บิทัล s
ออร์บิทัล s
![]()
![]()

click!
 |
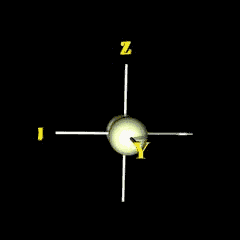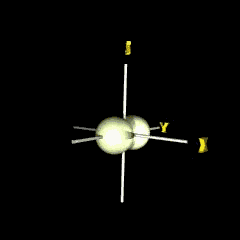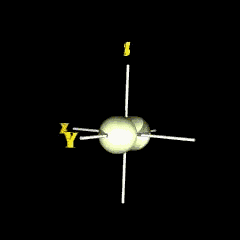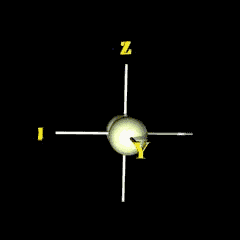
px
กลุ่มอิเล็กตรอนวางตัวตามแนวแกน x |
 |
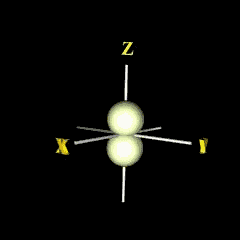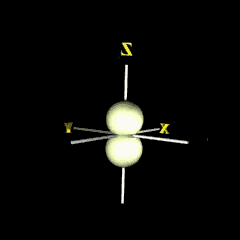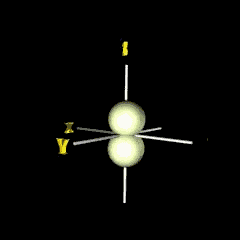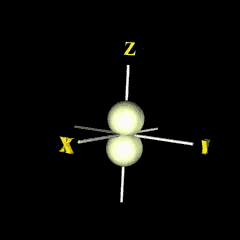
py
กลุ่มอิเล็กตรอนวางตัวตามแนวแกน y |
 |
pz
กลุ่มอิเล็กตรอนวางตัวตามแนวแกน z |


ออร์บิทัลอะตอม
ออร์บิทัลอะตอม
ออร์บิทัล s
ออร์บิทัล p
ออร์บิทัล d
ออร์บิทัล คือ บริเวณที่มีโอกาสพบอิเล็กตรอนตัวหนึ่งตัวใดมากที่สุด หรือบริเวณที่มีความหนาแน่นของอิเล็กตรอนมากที่สุด
การพิจารณาวงโคจรของอิเล็กตรอนรอบนิวเคลียสอาจแยกได้เป็น 2 ส่วน คือส่วนเชิงรัศมีและส่วนเชิงมุม
จากการแก้สมการคลื่น หาฟังก์ชันคลื่นในส่วนเชิงรัศมี Rn,l(r) เมื่อยกกำลังสองของฟังก์ชันคลื่นในส่วนเชิงรัศมี [ Rn, l(r) ]2 ย่อมหมายถึงโอกาสที่จะพบอิเล็กตรอนหรือความหนาแน่นของอิเล็กตรอนรอบๆนิวเคลียสที่ห่างจากนิวเคลียส r
1s, 2p และ 3d ไม่มี node แต่ 2s และ 3p มี 1 node (node คือ บริเวณที่โอกาสพบอิเล็กตรอนเป็นศูนย์) 2s และ 3p มี 1 node ส่วน 3s มี 2 node สำหรับอิเล็กตรอนทีมีค่า n สูงๆ โอกาสพบอิเล็กตรอนจะอยู่ห่างจากนิวเคลียสมากขึ้น ถ้า n เท่ากัน บริเวณใกล้นิวเคลียส โอกาสพบอิเล็กตรอนของออร์บิทัล s > p >d จากกราฟจะเห็นว่าบริเวณใกล้นิวเคลียส โอกาสพบอิเล็กตรอนของ 2s > 2p และ 3s>3p>3d
และจากฟังก์ชันคลื่นในส่วนเชิงมุม Yl , ml(q,f) ก็เช่นเดียวกัน กำลังสองของฟังก์ชันคลื่นในส่วนเชิงมุม [ Yl , ml(q,f)]2 จะหมายถึง โอกาสพบอิเล็กตรอนหรือความหนาแน่นของอิเล็กตรอนในทิศทางหนึ่งๆ (มุมqและfค่าหนึ่ง) พบว่าเฉพาะ s ออร์บิทัล (l=0) เท่านั้นที่โอกาสพบอิเล็กตรอนจะเท่ากันหมดไม่ว่ามุมqและfจะเป็นเท่าใด ส่วน p,d และ f ออร์บิทัล โอกาสพบอิเล็กตรอนจะต่างกันเมื่อ qและf ต่างกัน
สรุปรูปร่างของออร์บิทัลอะตอมที่ได้จาก [ Rn,l .(r)]2 และ [ Yl , ml(q,f)]2 ที่ระยะและทิศทางต่างๆจากนิวเคลียสเป็นดังนี้
เนื่องจากส่วนเชิงมุมในกรณีที่ l=0 เป็นเลขคงที่คือ 1 แสดงว่าการกระจายของอิเล็กตรอนเหล่านี้ไม่ขึ้นกับทิศทางหรือกล่าวได้ว่าเป็นการกระจายแบบทรงกลม (คือ เหมือนๆ กันหมดทุกๆ ทิศทาง) แต่ถ้า n มีค่าต่างกันการกระจายของอิเล็กตรอนที่ระยะต่างๆ จากนิวเคลียสจะแตกต่างกันด้วย ดังจะเห็นได้ว่าสำหรับ 1s ฟังก์ชันเข้าใกล้ศูนย์เมื่อ r มีค่ามาก แต่สำหรับ 2s ฟังก์ชันจะเป็นศูนย์ครั้งแรกที่ r = 2/k และเข้าใกล้ศูนย์อีกเมื่อ r มีค่ามากๆ (เพราะเทอม e-kr)
click!
รูปร่างต่างๆ ของ p-orbital
px
กลุ่มอิเล็กตรอนวางตัวตามแนวแกน xpy
กลุ่มอิเล็กตรอนวางตัวตามแนวแกน ypz
กลุ่มอิเล็กตรอนวางตัวตามแนวแกน z
เราเรียกบริเวณภายในรูปทรงแต่ละข้างของแกนว่า lobe ซึ่งมีเครื่องหมายตามฟังก์ชัน เช่น สำหรับ px-orbital ซึ่งมีฟังก์ชันเป็น x/r เมื่อ x เป็นค่าบวกหรือลบฟังก์ชันก็เป็นบวกหรือลบตามไปด้วย (เครื่องหมายนี้ไม่เกี่ยวกับประจุ) เช่นเดียวกับส่วนเชิงรัศมี ถ้าเราสนใจการกระจายของอิเล็กตรอน เราด้องนำ Y( q,f ) สำหรับ p -orbital มายกกำลังสอง จะได้รูปร่างใน 2 มิติ และ 3 มิติ ดังรูป
click!
รูปร่างต่างๆ ของ d-orbital